Key points

• Play the puzzle game Connectle here
• This game presents a rectilinear Steiner tree problem
• This problem is relevant to chip design

Introduction

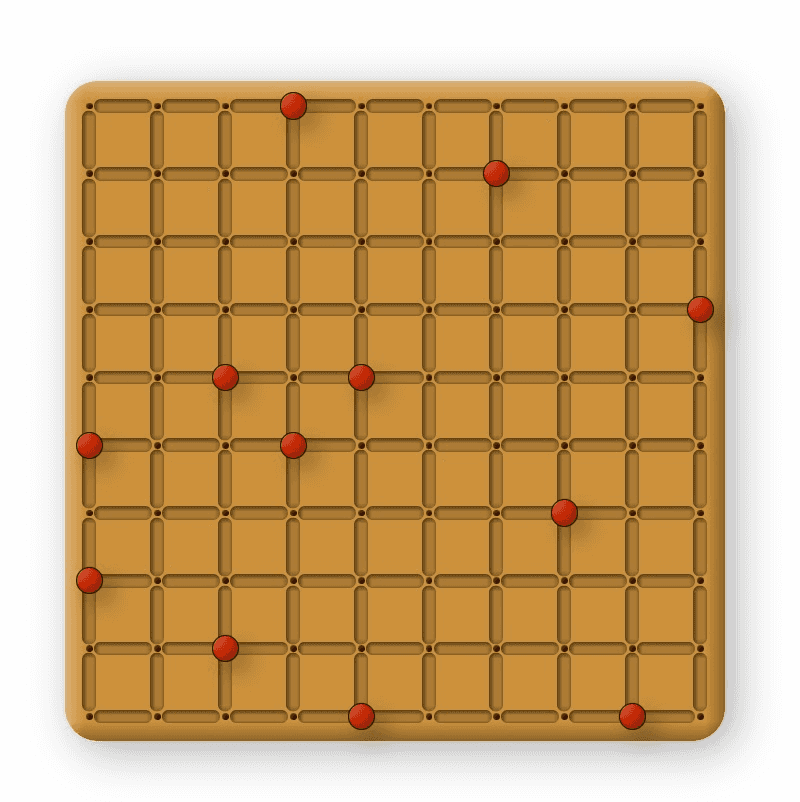
In 2023, I visited the Arithmeum, a mathematics museum, in Bonn with friends. We were particularly drawn by a puzzle game at the end of the venue. The game consisted of a board with a ten-by-ten grid, red pins to be placed at the intersections of the grid according to puzzles prescribed by a puzzle booklet, and blue path segments. The objective was simple: connect the pins using a given number of paths, but the challenge was fierce.

Some puzzles were so difficult we could not solve them with a group of friends, no matter how long we tried, always being one path short. First we randomly attempted to solve the puzzle based on randomness and gut-feeling, but when that failed we were forced to think and discuss how to tackle these challenges strategically and systematically.

Play the game

I have implemented this game in the browser (go fullscreen), so you can experience the challenge for yourself. Hopefully, this sparks curiosity to read more about the relevance of this problem, ways to solve these puzzles programmatically, and how this game and some of its added features were implemented.

Before we create new insights in this problem, let is consider the complexity of path finding. Then I will go over the steps to reproduce the board game digitally in three steps: 1) Copying the levels from the booklet, 2) Using an dynamic programming and an approximate algorithm to solve all puzzles and retrieve the Steiner points as hints. 3) Build the React App.

Path finding

Pathfinding is more than just a theoretical concept—it’s an essential part of our everyday lives. Whether you’re navigating the quickest route to the station, trying to find your way out of a maze, or planning the most efficient route to visit all the landmarks in a city, pathfinding is everywhere. While many of these challenges can be solved intuitively, some require sophisticated algorithmic solutions due to their complexity, scale, or time constraints. These problems are not just theoretical—they shape industries. Think about the pathfinding algorithms that control the movement of characters in video games, the robots navigating massive distribution centers to pick parcels, or the complex routing of electrical connections in computer chips.

In chip design, pathfinding is crucial for routing electrical connections between components while minimizing wire length and optimizing space. Unlike freeform paths, chip connections are restricted to right angles—much like the constraints found in Connectle’s puzzles. This restriction makes the problem particularly challenging and relevant to both recreational puzzle solvers and real-world engineers.

The mathematical challenge underlying these problems is the Rectilinear Steiner Tree Problem (RSTP). The objective is to connect a set of points (pins) with the shortest possible network of rectilinear paths, possibly introducing intermediate nodes called Steiner points. These additional nodes help reduce the overall wire length while adhering to the right-angle constraint, optimizing the solution. RSTP is an NP-hard problem, meaning that there is no known algorithm that can always find the optimal solution quickly. This mirrors the difficulty you may experience when tackling some of the tougher Connectle puzzles—both challenging for us to solve and for computers to compute.

Understanding pathfinding not only helps with solving puzzles like Connectle but also sheds light on critical concepts applied in technology. Here are three key principles that guide pathfinding in both gaming and real-world applications:

1. Manhattan Distance: In Connectle and similar problems, distances are calculated using Manhattan distance, which measures the total horizontal and vertical steps between two points. Unlike Euclidean distance, it fits with the rectilinear movement constraints, making it ideal for grid-based routing challenges in fields like urban planning, robotics, and chip design.
2. Steiner points: Steiner Points: Steiner points are additional nodes that can be strategically placed to reduce the total path length when connecting a set of points. By introducing these intermediate nodes, the overall distance can be minimized, leading to a more efficient solution. This technique is particularly valuable in circuit design, where reducing wire length can lead to lower costs and improved performance.
3. Approximate algorithms: Exact solutions to NP-hard problems like RSTP can be computationally expensive and time-consuming. Instead, approximate algorithms provide practical, efficient solutions by trading optimality for speed. Techniques such as greedy heuristics and randomized algorithms explore different variations of a problem to find solutions quickly, even if they’re not the absolute best. These strategies are essential both in solving Connectle’s puzzles and in addressing real-world engineering challenges.

Pathfinding in Connectle is more than just a puzzle — it’s an invitation to engage with real-world engineering concepts. By solving these challenges, you’re indirectly interacting with the same ideas that drive advancements in chip design, robotics, and beyond. Each Connectle puzzle mirrors a piece of a much larger problem: optimizing paths in the most efficient and creative way possible. As you work through these puzzles, you’re not only honing your problem-solving skills but also gaining an appreciation for how algorithmic thinking can improve both gameplay and real-world technologies. Who knows? The strategies and insights you develop here could spark innovation in fields far beyond the grid.

Copying the booklet

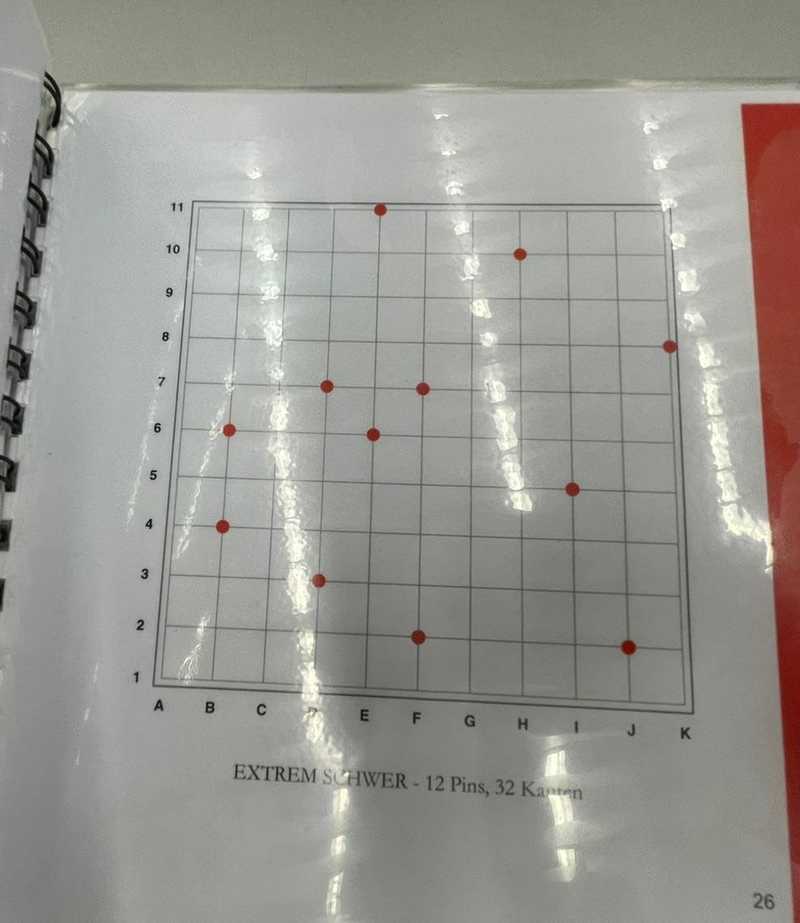
Recreating this game would not have been possible without a friend of mine taking photo’s of the puzzle booklet. At that point, neither of us had thought about reproducing the game, but later on, it was essential, as creating these puzzles, and specifically scoring them is notoriously hard.

Manually writing down the coordinate of up to 12 pins for 30 puzzles was no option. It would have been error-prone, and a single mistake could render a puzzle unsolvable. Therefor, first, aligned and rectified all photo’s by selecting three corner points in Matlab (see ginput). Then, I performed color correction to increase the red-white contrast. Finally, I again used ginput to get the row and column coordinates. At each grid intersection I measured the reddness and visualized the $n$ most red intersections. I stored these coordinates as JSON format to be read by the game. This process is shown below.

Raw photo Detected pins on rectified image In-game board

Solving puzzles programmatically

The solution to the game can be summarized as follows: Start by connecting the two closest pins. Then iteratively connect additional pins to existing pins or points along the paths until all pins are connected. To implement this solution, we will start with connecting two points and then apply this iteratively to connect all pins. We can than run this random approximation for many iterations to find a best solution. You can find the Python implementation of this solution on Google Colab.

Definitions: To implement this solution, let us define some key definitions: A point is a pair of integers $x, y$ where $x, y \in {0, 1, \dots, 9}$, a path consists of two points: $(\text{Point}_1, \text{Point}_2)$, and a pin is simply a specific type of point.

The first we need to be able to connect two points. The larger the distance between the points, the more complex our routing options are: $O(x_2 - x_1) × (y_2 - y_1)$. To reduce complexity each pair of points is connected using a right-angle path. For example, to connect $(x_1, y_1)$ to $(x_2, y_2)$, the path moves horizontally along the $x$-axis first, then vertically along the $y$-axis. Thus, the random order in which the points are provided determines the direction of this angle.

Second, we need to find out which points to connect. The function $\text{find\_closest\_points}$ sorts all possible connections by increasing Manhattan distance. It then selects a pair from the top-$rng$ at random.

We can now run the $\text{find\_closest\_points}$ and $\text{connect\_two\_points}$ functions iteratively until all points have been connected.

Since the solution involves some randomness, we might need to repeat the process multiple times to achieve the desired number of paths. This is handled using an iterative search that evaluates up to a specified maximum number of attempts. If a valid solution is found, it is returned; otherwise, an empty set is returned.

By iteratively building connections based on proximity and leveraging randomness to explore variations, this method is both efficient and robust for solving path connection puzzles. The combination of deterministic logic with stochastic elements ensures adaptability across different configurations.

Building the React Game

After my experience with building the game Pickomino (or Regenwormen in Dutch), creating this game was relatively straight-forward.

I had a lot of fun with creating the fully parameterized CSS design. Single parameter changes in the master file, such as the grid size, pin size, and path dimensions, were programmatically applied throughout the code. This made it easy to tune the design of the game to match the design of the board, but it also made it easy to switch to a 9-by-9 grid, after I found out that one row and one column are never occupied by any puzzle. Finally, this made it simple to create the URL preview for the game. So I am very happy about this property.

The major challenge in the Pickomino game was the synchronization of React states. This was again a challenge to the verification of the solution because it was essential not to verify anything but the latest game state. The verification of the solution consists of three statements: 1) Was the right number of paths used? 2) Are all paths connected? 3) Are all pins reached? I built a visual debug mode with enabled me to visually inspect that these states are correctly set during play-testing. I will also do this in future projects, as it greatly improved the stability of the code.

Conclusion

Connectle offers a unique blend of entertainment and intellectual challenge while subtly introducing the complexities of pathfinding. From its origins as a captivating museum game to its digital recreation, the project highlights how recreational puzzles can intersect with real-world engineering problems like chip design. Implementing the game provided insights into algorithmic problem-solving, including Manhattan distances, Steiner points, and approximate algorithms, showcasing the balance between simplicity and computational ingenuity.

By blending gameplay with programmatic solutions, Connectle invites players to experience the challenge firsthand while exploring how such puzzles relate to practical applications. Whether you’re solving for fun or diving deeper into the algorithmic underpinnings, this journey underscores the timeless appeal of puzzles and their surprising relevance to modern technology.